Graph::Function, a gem for graphing functions

When I do katas I often do several iterations with a focus on performance. I think this is probably pretty common. You start off with some quadratic solution, ponder a bit, and then try to get down to linear or n log n performance¹.

But there’s also stuff like, in Ruby at least, discovering the cost of dynamic Array allocation in the execution of your algorithm. In other words sometimes you forget your language has some abstractions that have real costs.

Although I’d like to also get better at algorithmic analysis from a purely formal place, in the meantime I’ve found graphing functions super useful. I found it so useful that I’ve written a gem, Graph::Function, to make it easier to pop a comparison into an exercise I’m working on.

Here’s an example of using the library with some exercise code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
require 'graph/function'
Graph::Function.as_gif(File.expand_path('../comparing.gif', __FILE__))

def bubble_sort(array)
  n = array.length
  loop do
    swapped = false
    (n-1).times do |i|
      if array[i] > array[i+1]
        array[i], array[i+1] = array[i+1], array[i]
        swapped = true
      end
    end
    break if not swapped
  end
  array
end

def sort(array)
  array.sort
end

Graph::Function::IntsComparison.of(method(:sort), method(:bubble_sort))

And here’s the graph we generated:

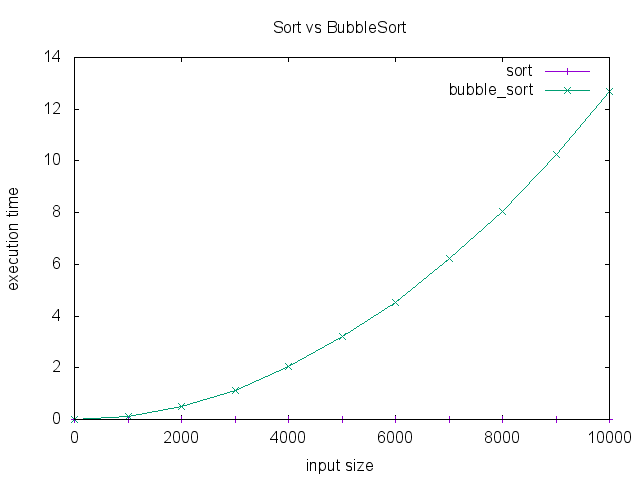
As you can see, implementing bubble_sort yourself doesn’t run as fast as Ruby’s own sort. (Hopefully not too surprising.) But it was very easy to generate a helpful graph to demonstrate that, right?

I hope you’ll get some utility out of this gem, and if you have any thoughts about its direction feel free to discuss it in the issues.