table driven methods
I read parts of Code Complete a year or so ago and one of the sections I found kind of intriguing was Table-Driven Methods.
I always found the example in the book a bit dense, and not found many examples online that I felt were tractable. But this weekend I happened upon a good case to use a TDM, so I figured I would document it. I’m not an amazing Javascript programmer so as to the style of my implementation, well, caveat lector!
The example problem to solve I’m going to use is Conway’s Game of Life. I’d not programmed it before myself and it was pretty fun to do. Its ruleset affords us a good opportunity to implement a TDM because it’s slightly non-trivial conditional logic that is still short enough to keep in mind as we go.
Here’s the rules I copied from Disruptive Communications’s blog post on GOL:
- If a dead cell has exactly three live neighbours, it comes to life
- If a live cell has less than two live neighbours, it dies
- If a live cell has more than three live neighbours, it dies
- If a live cell has two or three live neighbours, it continues living
It doesn’t really matter if you don’t know the domain of this problem as
long as you have a feeling for how to translate those rules into code.
Reading through these rules, I can easily imagine a complicated switch
or set of if/else statements to capture the logic. Like you have some
outer if/else for the liveness or deadness of a cell, and then some
additional statements within the liveness branch to codify the rest.
But at base, we really have 2 dimensions of logic that are fully and independently enumerable into very small sets. We can actually put all these values in a table.
One dimension, our “outer” dimension, is whether a cell is alive or dead. If we think of a prototypical xy graph and x is the horizontal dimension, then the values of x are “livingCell” and “deadCell” or we could define them as integers like 0 and 1.
| livingCell | deadCell |
|---|---|
| ???? | ???? |
We get this outer dimension from this portion of our ruleset:
- If a dead cell …
- If a live cell …
- If a live cell …
- If a live cell …
The other dimension (our “y” dimension or the row numbers of our table) is the number of live neighbors.
| (numberOfLiveNeighbors) | livingCell | deadCell |
|---|---|---|
| 0 | dead | dead |
| 1 | dead | dead |
| 2 | live | dead |
| 3 | live | live |
| 4 | dead | dead |
This corresponds to this portion of our ruleset:
- … exactly three live neighbours, …
(
== 3) - … less than two live neighbours, …
(
== 0 || == 1) - … more than three live neighbours, …
(
== 4) - … two or three live neighbours, …
(
== 2 || == 3)
Both dimensions can be expressed as simple integers if we clamp the live
neighbor count at the minimum and maximum relevant ns (for our ruleset,
0 and 4).
I’m going to work inside out and start with the inner dimensions dependent
on live neighbor count. Here’s how I grab that count, which is only
important because by
clamp,
numberOfLiveNeighbors is guaranteed to be some value between 0 and 4.:
1
2
3
4
// get the liveness of every neighbor of the cell I care about
var neighborhood = getNeighbors(i).map(function(e) { return isLive(grid, e); });
// filter them for only true values (for live cells)
var numberOfLiveNeighbors = neighborhood.filter(utils.identity).length.clamp(0, 4);
Using live neighbor count as our index key, we need to encode the
conditions of the dimension. For instance, one condition is that we
know a live cell with less than 2 neighbors will die, so the 0 and
1 position of a live cell’s potential states should both be 'dead':
1
2
3
4
5
6
// 0 and 1 are valued 'dead', because of rule #2
var nextLivingState = ['dead', 'dead', 'live', 'live', 'dead'];
// coincidentally, so are 0 and 1 for a dead cell
// all of the dead cell states are owing to rule #1
var nextDeadState = ['dead', 'dead', 'dead', 'live', 'dead'];
If we didn’t have an additional dimension of whether the cell is alive or dead itself to begin with, we’d only need one of the two Arrays defined above, and could index directly into it. Since cells can be alive or dead, we need to encode that too in another Array. The simplest thing to do is to map dead states to 0 and live states to 1 in the “outer” “y” dimension as I described above:
1
2
3
// nextPossibleState[0] <==> dead
// nextPossibleState[1] <==> alive
var nextPossibleState = [nextDeadState, nextLivingState];
Now we can just index in to that data structure based on whether the
current cell is alive (isLive(grid, i)) first and how many live
neighbors it has (numberOfLiveNeighbors) second:
1
2
var nextState = nextPossibleState[isLive(grid, i)][numberOfLiveNeighbors];
// for instance: nextPossibleState[0][4] => 'dead'
Based on the nextState I calculate the new value of a cell on the next
“turn” in the GOL, though if you wanted, there’s no reason not to collapse
this final step into the data structure we created.
To do so, you could directly call a method based on where you index in to, like so:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// what we'll ultimately do to a cell depending on our conditional logic
function live(cell,i) {
cell.push(compass.positionFromId(i));
}
function dead(cell) {
cell.length = 0;
}
// our conditional logic encoded into Arrays
var nextLivingState = [dead, dead, live, live, dead];
var nextDeadState = [dead, dead, dead, live, dead];
var nextPossibleState = [nextDeadState, nextLivingState];
// indexing into our conditional logic based on cell state and neighbor state
nextPossibleState[isLive(grid, i)][numberOfLiveNeighbors].call(null, cell, i);
My working code is here. It’s nothing special, but it’s a live example of how to make use of a TDM. I think in the right place, a TDM makes the code easier to read and understand. They also can perform a little better; like, trivially better in my tests anyway. Here’s a performance comparison in Ruby:
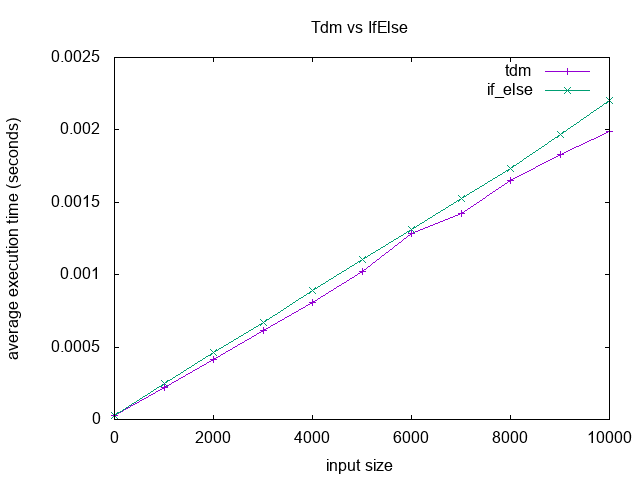
Table Driven Methods are cool, so why not use them all the time everywhere? Well, here is the memory performance of my initial, naive implementation in Ruby:
1
2
3
4
5
6
7
8
9
10
11
Calculating -------------------------------------
tdm 792.000 memsize ( 0.000 retained)
12.000 objects ( 0.000 retained)
0.000 strings ( 0.000 retained)
if_else 568.000 memsize ( 0.000 retained)
9.000 objects ( 0.000 retained)
0.000 strings ( 0.000 retained)
Comparison:
if_else: 568 allocated
tdm: 792 allocated - 1.39x more
Table driven methods make use of Arrays, which are managed (allocated) on the heap. While a case statement or if/else construct may not read as nicely (to me) they have the advantage of being managed on the stack1. That can have performance benefits not reflected directly in execution speed.
I think this allocation difference is not a deal-breaker (though not insignificant at a 39% increase in my test), but if you were suddenly using TDMs for every single call, that could add up. Imagine a 39% memory tax on every single call: not a good look.
We can definitely do better than paying that tax on every call. Here’s the TDM when I move those Arrays out as frozen constants (I also moved the procs out for both methods, to reduce noise):
1
2
3
4
5
6
7
8
9
10
11
Calculating -------------------------------------
tdm 280.000 memsize ( 0.000 retained)
6.000 objects ( 0.000 retained)
0.000 strings ( 0.000 retained)
if_else 280.000 memsize ( 0.000 retained)
6.000 objects ( 0.000 retained)
0.000 strings ( 0.000 retained)
Comparison:
tdm: 280 allocated
if_else: 280 allocated - same
We are still allocating the Arrays, but only once, rather than on every
call. That’s better, but it still cost us when
we loaded our program. freeze can’t save us there. This is because Ruby’s freeze
behavior is different for String and Array:
1
2
3
4
5
Benchmark.memory {|x| x.report { "foo".freeze } }
Calculating -------------------------------------
0.000 memsize ( 0.000 retained)
0.000 objects ( 0.000 retained)
0.000 strings ( 0.000 retained)
For String, no object was allocated, but for Array, it will be:
1
2
3
4
5
Benchmark.memory {|x| x.report { [1,2,3].freeze } }
Calculating -------------------------------------
40.000 memsize ( 0.000 retained)
1.000 objects ( 0.000 retained)
0.000 strings ( 0.000 retained)
This does suggest one final, perhaps a bit goofy, improvement you can make: use Strings instead of Arrays!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# procs that match chars
D = proc {|x| p "#{x} is dead".freeze }
L = proc {|x| p "#{x} is live".freeze }
# dead states, then live states
next_state_string = "DDDLDDDLLD".freeze
# our main index into the next state
number_of_live_neighbors = 3 # clamped at 4
# how many states do we need to move in if we're alive?
LIVENESS_OFFSET = 4
chosen_proc_name = next_state_string[number_of_live_neighbors + LIVENESS_OFFSET]
Object.const_get(chosen_proc_name).call(1)
# => "1 is live"
Here’s the memory performance difference between the TDM and a “SDM” (String Driven Method):
1
2
3
4
5
6
7
8
9
10
11
12
13
Calculating -------------------------------------
"1 is live"
SDM 561.000 memsize ( 0.000 retained)
6.000 objects ( 0.000 retained)
4.000 strings ( 0.000 retained)
"1 is live"
TDM 721.000 memsize ( 0.000 retained)
8.000 objects ( 0.000 retained)
3.000 strings ( 0.000 retained)
Comparison:
SDM: 561 allocated
TDM: 721 allocated - 1.29x more
To my mind, it’s sufficient to make sure to allocate your “table” outside of the method itself. But it’s fun to see the alternative.
-
Hat tip to my colleague Nick Thompson to humoring me, as always, in thinking through those tradeoffs. ↩


